Maple如何计算函数的极限、导数和积分

发布时间：2025-08-20 12:38:01作者：xx

maple是一款功能强大的数学软件，在计算函数的极限、导数和积分方面表现出色。

函数极限的计算

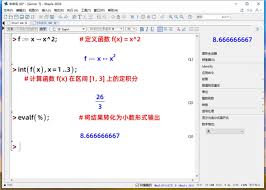
在maple中，使用limit函数可以方便地计算函数的极限。例如，对于函数$f(x)=⁄frac{x^2 - 1}{x - 1}$，求当$x$趋近于1时的极限。只需在maple中输入limit((x^2 - 1)/(x - 1), x = 1)，即可快速得到结果2。它不仅能处理简单的代数函数极限，对于三角函数、指数函数等复杂函数的极限计算也十分高效。比如，计算$⁄lim_{x ⁄to 0} ⁄frac{⁄sin x}{x}$，输入limit(sin(x)/x, x = 0)，就能得出结果1。

函数导数的求解

maple的diff函数可用于求函数的导数。若要对函数$y = x^3 + 2x^2 + 1$求导，输入diff(x^3 + 2*x^2 + 1, x)，就能得到导数$3x^2 + 4x$。对于复合函数求导，它也能轻松应对。例如，对于函数$y = ⁄sin(2x)$，输入diff(sin(2*x), x)，可得到$2⁄cos(2x)$。而且，maple还能求高阶导数。如求函数$y = e^{x^2}$的二阶导数，输入diff(exp(x^2), x, 2)，即可得出结果$(2 + 4x^2)e^{x^2}$。

函数积分的运算

利用int函数可以进行函数积分运算。计算函数$f(x)=x^2$在区间[0, 1]上的定积分，输入int(x^2, x = 0..1)，可得到结果$⁄frac{1}{3}$。对于不定积分，如求$⁄int ⁄cos x ⁄, dx$，输入int(cos(x), x)，能得到$⁄sin x + c$（其中$c$为常数）。maple在处理复杂的积分式子时优势明显，无论是有理函数积分、三角函数积分还是指数函数积分等，都能通过其强大的算法给出准确结果。比如，计算$⁄int ⁄frac{1}{x^2 + 1} ⁄, dx$，输入int(1/(x^2 + 1), x)，可得到$⁄arctan x + c$。

总之，maple为函数的极限、导数和积分计算提供了便捷、高效且准确的解决方案，是数学学习和研究中的得力工具。

免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。

上一篇：小鹰看看如何注销账号

下一篇：ps如何制作云朵飘动效果动画